The city of Königsberg was built on the banks of the Pregel River. The river created two islands within the city, which were connected to the mainland through seven bridges. The question arose whether it was possible to cross all seven bridges exactly once.
At some point, Leonhard Euler encountered this problem and presented a solution on August 26, 1735 — it was not possible. In answering this question, Euler laid the foundation for a whole new branch of mathematics: the study of graphs.
A graph consists of two types of objects: vertices (also known as nodes or entities) and edges (also known as relationships or arcs). A path in a graph is a sequence of edges that connect a sequence of nodes.
In this case, each node represents a land mass, and each edge represents a bridge. By traversing the graph, we form a path. Since each edge can be traversed both ways, this graph is undirected. Additionally, since we can start at one node, traverse the graph, and return to the same node, it forms a cyclic graph. The goal is to find a trail through the graph that only crosses each edge once — this is called an Eulerian path or Eulerian walk
Euler observed that when you enter a landmass, you must also leave it unless it is the start or end of your walk. Therefore, a landmass must have an even number of bridges (one to enter and one to leave) to meet this criterion.
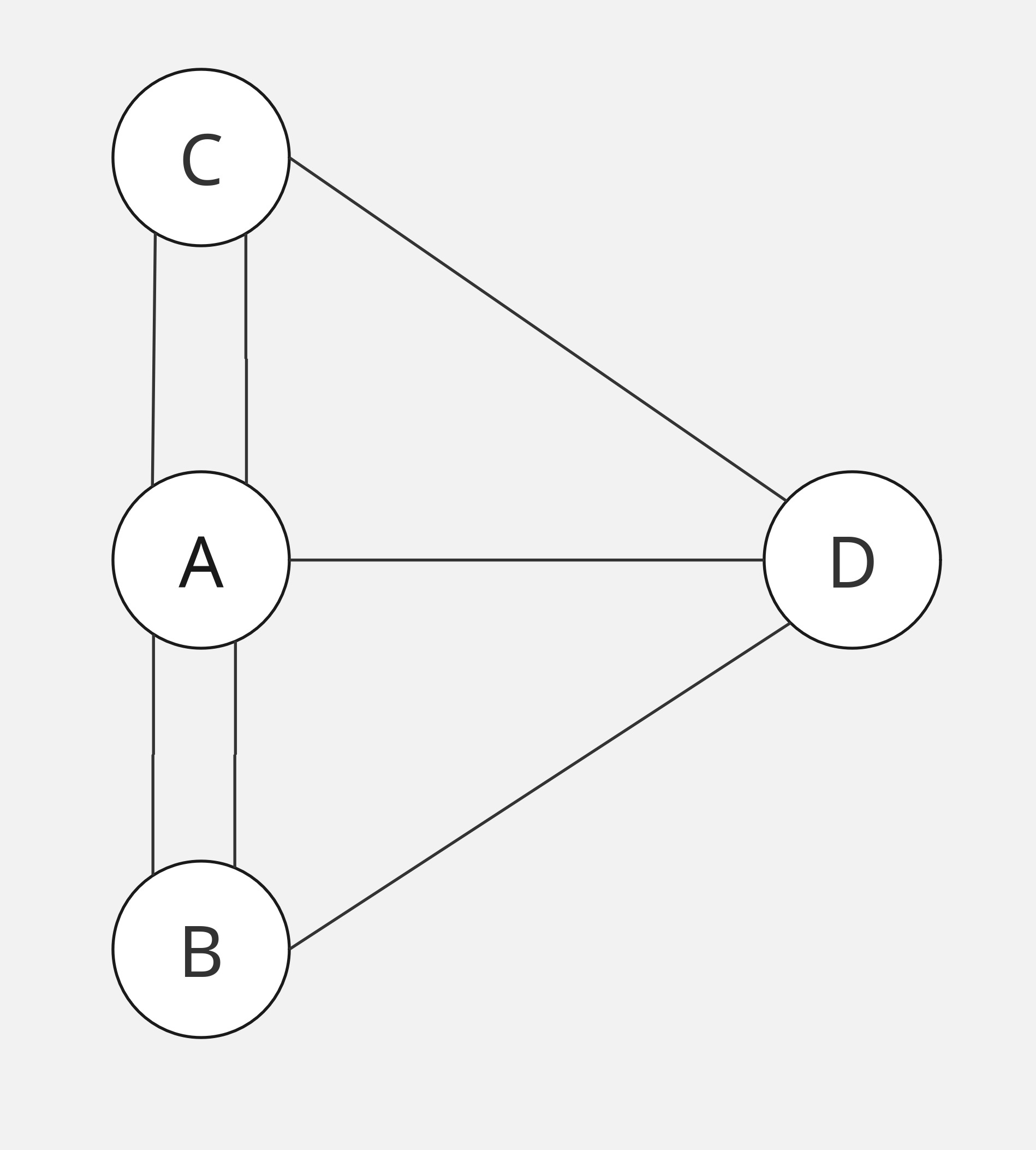
There are seven bridges connecting these areas:
- A has 5 bridges connected (odd degree).
- B has 3 bridges connected (odd degree).
- C has 3 bridges connected (odd degree).
- D has 3 bridges connected (odd degree).
According to Euler’s theorem, for an Eulerian path to exist, the graph must have either 0 or 2 vertices of odd degree (the number of edges connected to the vertex). However, in the Königsberg bridge problem, all four land masses (nodes) have an odd degree (3 or 5), making it impossible to construct an Eulerian path or circuit.
Thus, it is mathematically impossible to cross all seven bridges exactly once and return to the starting point.
References
- Louridas, P. (2017). Algorithms: A New Approach. The MIT Press.
- Kleppmann, M. (2017). Designing Data-Intensive Applications. O’Reilly Media.
- Wikipedia. (n.d.). Seven Bridges of Königsberg. Retrieved from https://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg

